|
|
|
Return to Electron Orbits Home Page
A Description for Discrete Electron Orbits about the Atomic Nucleus
Carl Segor
June 19, 2000
April 27, 2002
Copyright 2000-2006 Carl Segor - All rights reserved
Abstract - While the Schrodinger equation has been very successful toward describing atomic behavior, its mathematical form was not constructed from a conceptual model. Rather it is an equation that meets a set of constraints. And, though the Rutherford model was conceptually attractive, several deficiencies arose prompting its replacement by the Schrodinger equation. In our pursuit to describe nature, it is important that our mathematical representations are derived from conceptual models consistent with fundamental principles. The discrete orbits taken by electrons are one such phenomenon of nature and that, which this paper seeks to resolve.
1.0 Introduction
When Ernest Rutherford proposed the "planetary" model to describe the atomic structure, it represented a familiar conceptual representation. However, it was not clear why electrons should stay in orbit and not spiral into the nucleus, as they lost energy through radiation. Niels Bohr proposed that the angular momentum could only take on integer multiples of Planck's constant. In asserting this proposal, he digressed from the physical model and was stating that the electron will not radiate when it has these values of angular momentum. Though his postulate was correct, it is possible to derive these stable orbits from the original Rutherford model.
However, before deriving an equation, several sections will be devoted to background material. First, one of the deficiencies of the model will be addressed followed by several logical arguments to support the model.
1.1 The Uncertainty Principle and the Rutherford Model
One of the arguments leveled against the "planetary" model is that it violates the Uncertainty Principle. The electrons are described as having a specific position and momentum (mass * velocity), while the uncertainty relationship, DxDpx > h/4p, says that you can not know this. The Uncertainty Principle, of which the uncertainty relationship is one of its mathematical expressions, arises from the fact that every measurement disturbs that, which is measured. When the flight of an electron is measured by the response of nearby electrons via their electric fields, the flight must be disturbed and thus prevent us from knowing its precise position and velocity. But does this mean that the electron actually exists in a state of uncertain condition? Or, is it the case that, its position and momentum are uncertain to the human observer, but that they exist in a very specific condition. Proponents of the former place the observer at the center of the universe. They assert that, because an observer is unable to measure particle conditions (i.e. momentum and position) with greater precision than the limit of the uncertainty relationship, that the particles themselves (i.e. electrons) must follow. It is correct for an observer to say that an electron has the probability to be in a certain place. This statement is not in error, because with incomplete knowledge one must account for the possibilities not covered by what is known. What is a statement of error is to say that the electron is "spread out" or that the "electron wave function collapses". How does an observer acquiring knowledge give form and existence to an entity that precedes him? The following example demonstrates how two interpretations, may be made of a system. A transceiver at position A transmits a light pulse to the sphere at B, which reflects it. Once the transceiver has moved to C, it has had the chance to receive a set of reflected signals that originated from A. One analyst is provided with the model and told to explain. He considers the spherical object's size and derives the equation shown in the illustration (Note: If image is not clear, many browsers allow viewing the image directly. For example with Netscape, right mouse button click on the image, then select "view image").
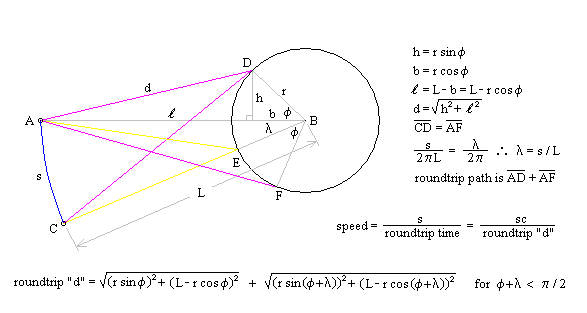
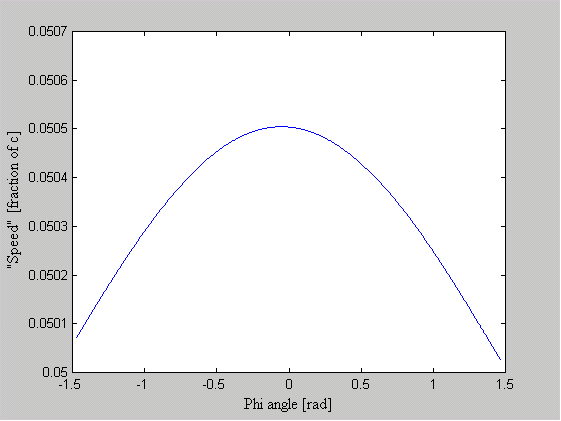
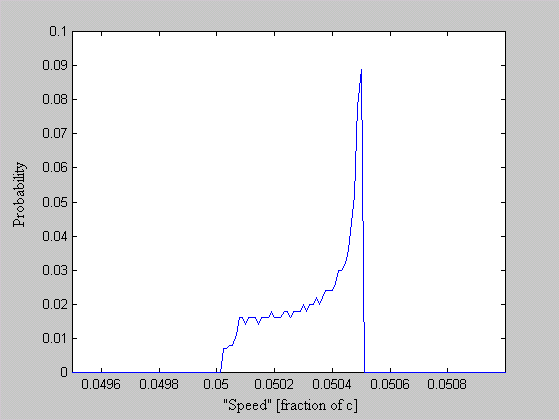
Figure 1 Effect of Path Delay on Apparent "Speed"
Next, another analyst is given the speed plots based on the roundtrip time interval as well as the probability distribution of those speeds. He may conclude that, if the objects are considered to be points whereby the roundtrip time is single valued, then the transceiver's position and velocity is uncertain. The choice the second analyst must make is whether or not to describe the objects themselves as entities that either have, or do not have, size. What is apparent from this example is that the information (position, momentum, etc) reflected by the spherical object, when the transceiver is at A, is not communicated in the same instant as it moves to position C.
1.2 Particles have Size
Most references define mass as the resistance matter exhibits to any change in its motion. Certainly the question must arise - why? Why should matter resist at all? What characteristic of matter "senses" that it is being moved? A definition of matter is needed and will be defined as specific states of the properties of space.
At some level, a primitive particle of matter exists, which can be no longer defined as being made of other matter. This fundamental unit will be referred to as an elemental massive particle (EMP)1. Since some smaller form of matter can not define the EMP, another conceptual representation is necessary. The following argument is presented:
premise: Matter can not travel at the speed of light, hence, EMPs can not travel at the speed of light.
proposition: The speed of light marks the surface boundary of an EMP.
conclusion: Therefore, EMPs can not exist inside each other (i.e. they can not occupy the same position in space).
The premise and conclusion are facts we already accept about matter; the proposition supports the conclusion. It asserts that the boundary of an EMP is characterized as having the constraint that the speed of light is the only legal velocity. We can visualize a spherical surface (i.e. a surface with 3D symmetry) that demarcates a boundary between the "inside" and outside of the EMP, where the line of demarcation is "c". Further, spherical shells of increasing radius and decreasing speed may be drawn surrounding the EMP and speculatively the converse, shells of decreasing radius and increasing speed within it. To an outside observer, the EMP has a size set by the boundary surface (analogous to the Schwarzschild radius attributed to a black hole) and a "charge". Thus, every EMP has size and charge, while every neutral massive particle (ex. neutron) is a "molecule" of EMPs (i.e. two or more EMPs are required to make up a neutral particle).
We now come to define space as separation with the consequence that space may be said to have the properties of distance and temporality. Clearly, either distance or time may be used as a measure of separation, yet they are separate dimensions. The usual descriptor, space-time, is thus replaced simply by - space. As an analogy, we may consider a rectangle of constant area to be comparable to space. This is to say that each has two properties: the rectangle - length and width, and space - distance and 1/time. Its area is comparable to the speed of light (i.e. the product of its properties) and the line comparable to a particle where the state of one property approaches zero. Specifically, an EMP represents properties of space where 1/time at the boundary surface approaches zero. Therefore, where space exhibits the qualities of its properties as described, matter is said to be present. Once space is understood to have the properties of distance and temporality, it is possible to described matter in a fundamental way.
It will now be shown that mass can be understood to occur, because matter "occupies" space (i.e. mass is a result of matter having size). A thought experiment serves as a demonstration. The experiment begins by accepting the premise that a "mass-less matter" exists, then proceeds until the conclusion contradicts the premise. In this way it shows that matter must have mass because it occupies space.
A scientist discovers a new material, which is massless and, once formed, incompressible. A project is undertaken to create an extremely long spaghetti shaped object (for purposes of this discussion, it may be considered infinitely long) out of this material. Once completed, a force is applied to one end of the object with the consequence that it does not move! Since it takes time (infinitely long) for the applied force to travel down and back along the object at the speed of light, the object has acquired "mass" (that is, the ratio of the applied force to the acceleration the object exhibits). At the elemental level of a massive particle, mass is the effect, which arises from the delay incurred by the force propagating through the particle2. The ratio of mp to me suggests that this is indeed the case, as it is equal to the ratio of the particle diameters3. Mass at the macroscopic level thus arises from the volumetric attraction of all particles within the solid.
1.3 Special Relativity
This section presents an alternate form of the Special Relativity equations, which will assist in the derivation of discrete atomic orbits. Length contraction and time/momentum dilation formulas are presented:
d' = d ( 1 - s2/c2 )0.5 length contraction
t' = t / ( 1 - s2/c2 )0.5 time dilation Equation 1
p' = p / ( 1 - s2/c2 )0.5 relativistic momentum
where:d', t' and p' are the moving frame's contracted length, dilated time and momentum
d, t and p are the "proper" length, time and momentum (for p it is m0v)
s is the moving frame's speed
c is the speed of light
Recognizing that the term, (1 - s2/c2 )0.5, is the Pythagorean Theorem for right triangles, we may equivalently say:
(1 - s2/c2 )0.5 = (c2 - s2 )0.5 / c = c cosq / c = cosq
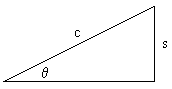
c cosq or (c2 - s2 )0.5
Hence, we may develop the alternate form:
q
= asin(s/c) speed angle Equation 2d' = d cos(q ) length contraction
t' = t / cos(q ) time dilation
p' = p / cos(q ) relativistic momentum Equation 3
1.4 Discrete Orbits of the Atomic Nucleus
What has been presented up to this point is:
From here we are prepared to derive from the Rutherford model, an equation which predicts the stable orbits of the hydrogen atom.
There are three fundamental ways to view the electron/proton relationship. That is, an observer can align himself with any one of three possible translational reference frames4 - the proton's, the electron's or neither. The typical view is to place the observer at rest with respect to the proton, since it is the most massive. In this case, the electron orbits the proton as is shown in Figure 2 having momentum pe (pte at A in the figure) directed in the -y direction. The proton reacts with opposition to the electron and produces momentum pp (at B) directed in the +y direction. The proton, however, responds not to pe, but to the relativistic momentum, pe'. In turn, the electron reacts to pp (at C).
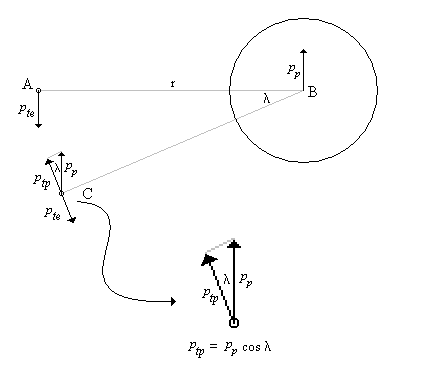
Figure 2 - Delayed Momentum and its Effect on the Electron
An equation may be written to represent the relationship at C which states that the electron's momentum plus the proton's momentum plus the momentum lost to space (i.e. light) is zero.
pe + pp + pspace = 0
This equation may be separated into two pieces - the momentum directed radially and the momentum directed tangentially.
pre + prp + prspace = 0
pte + ptp + ptspace = 0
If we accept that a condition exists where the momentum lost to space is zero (that is, no light is radiated, which is consistent with observation), then the following equations would have to hold:
pre + prp = 0
pte + ptp = 0
With the tangential components balanced, we can derive the following:
pte = - ptp
pte = - pp cos l
pte = - (- pte / cos qe ) cos l
where: qe is the speed angle associated with the electron and
pp = - pte / cos qe (see section 1.3, equation 3)
cos l = cos qe
l
= qeThe angle, l, is the orbital travel distance of the electron over the path A to C divided by the circumference of the orbit times 2p to get the angle in radians. The distance the electron travels is the round-trip time it takes for the momentum of the electron to be communicated at the speed of light to the proton and back. The speed angle, qe, on the right is simply asin(se/c) as described in section 1.3, equation 2.
2p (2t'se) / (2pr) = asin(se/c)
where:2t'se is the distance the electron travels with 2t' being the roundtrip time and se the electron's speed.
2pr is the orbital circumference.
2se (t' / r) = asin(se/c)
sin(2se (t' / r)) = se/c Equation 4
Since acceleration is associated with the electric field, time "slows down" as the "surface" of the charged particle is approached. Therefore, the time for the information about the electron's momentum to get to the proton (i.e. t' - one half of the round-trip time) may be expressed as an average. Since, from section 1.3 equation 1, t' = t (1 - s2/c2)-0.5, its average would be defined as:
tavg' = [ t abò(1 - n 2)-0.5 dn ] / (b-a)
where: n = s/c [no units]
Recall that n is a speed ratio, devised to calculate the time to convey the momentum. If s is zero, as would be the case for t' being the same as t, then n would also be zero. That is, where no time dilation is present, the relativity factor, (1 - n 2)-0.5, is one. So the lower limit of integration, a, is zero5.
tavg' = [ t 0bò(1 - n 2)-0.5 dn ] / b
It is the upper limit of integration, b, which must now be considered - the upper "speed" over which the momentum is transferred. Recall from section 1.1, that due to different path lengths, the speed was distributed over a range. In effect, the momentum of the electron at A does not affect the proton in a single instant. Though it is understood that the different speeds are the result of different path delays caused by the size, charge and mass of the proton, we choose to represent the arrival time of the momentum information at point B by different speeds in order to solve for an average time. It is only the general form of the equation, which is being sought now. Later, when the general form is complete, an actual value for "b" will be obtained.
The exact form of the speed distribution is not necessarily relevant. Whether it is an exponential, bell, triangle, cycloid, or flat, what is important is that a speed exists that spans to 50% of the speeds. This "mean speed" will be labeled, a . Thus, 2a will span 100% of the possible speeds that are present.
tavg' = [ t 02aò(1 - n 2)-0.5 dn ] / 2a
Performing the integration we have:
tavg' = t [ asin(n ) ]02a / 2a
tavg' = t/2a [ asin(2a ) - asin(0) ] = (t/2a ) asin(2a )
where: asin(2a ) = ( np + (-1)n q )
tavg' = (t/2a )( np + -1nq )
Substituting into equation 4:
sin(2se ((t/r2a )( np + -1nq ))) = se/c
Realizing that t/r is 1/c:
sin(se/c ((1/a )( np + -1nq ))) = se/c
sin((h /a )( np + -1nq )) = h Equation 5
where: h = se/c
Remember that the initial observation was, if momentum lost to space was zero, then the momentum of the electron would be exactly cancelled by the time delayed momentum of the proton. Equation 5 represents the electron speeds that are able to satisfy this condition, where h = se/c, a is the mean speed of the momentum exchange and q is the numeric value of the asin(2a). Taking measurements from nature, the unknowns a and q can be set. The hydrogen atom's diameter is approximately 1.0584e-10 meters. The electrostatic force of attraction is F = e2/4pe0r2. The centripetal force is mse2/r. When the centripetal force and electrostatic forces are in balance:
e2/4pe0r2 = mse2/r
se = (e2/4pme0r)0.5 Equation 6
where:e = 1.602176e-19 [C]
m = 9.109382e-31 [kg] 6
e
0 = 8.854e-12 [C2N-1m-2]r = 0.5292e-10 [m]
se = 2.187667e6 [m/s]
h
= se/c = 7.29727e-3Numerically solving for a and q when n = 1:
sin((7.29727e-3/a )(p - q )) / 7.29727e-3 = 1
a
= 7.28036e-3q
= 1.45612e-2 [rad]We now consider that a and q are constant and that a numerical solution exists where h satisfies equation 5 for various values of n. Figure 3 shows overlaid plots of h for n = 1, 3 and 6 of the equation:
[sin((h /a )( np + -1nq ))/h ] - 1 = 0 Equation 7
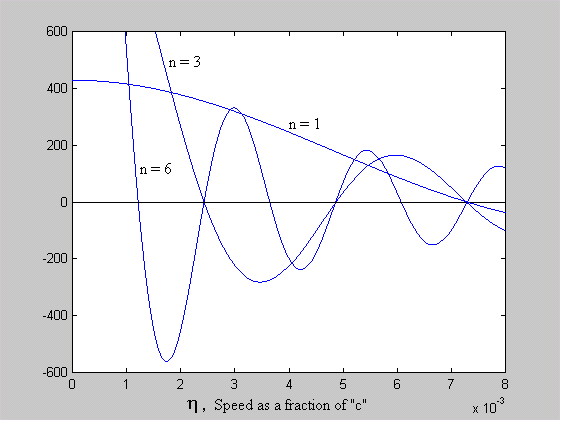
Figure 3 - Predicted Discrete Orbits of the Electron
Where each plot crosses the x-axis (i.e the solution to equation 7 is zero), a stable orbit exists. The value of h at these zero-crossings corresponds to a radius given by:
e2/4pe0r2 = mse2/r
e2/4pe0c2 = mse2r/c2
e2/4pe0c2 = (me0/cosqe)(h 2r)
e2/4pe0me0c2 = (h 2/cosqe)r
K = r (h2/cosqe)
where: K = e2/4pe0me0c2
K = r (sin2(qe)/cosqe)
where: sinqe = h
K = r tanqesinqe
r = K / tanqesinqe [m] Equation 8
For n = 1 through 6 the radii in meters are:
|
n = 1 |
n = 2 |
n = 3 |
n = 4 |
n = 5 |
n = 6 |
|
0.5291e-10 |
0.5279e-10 |
0.5308e-10 |
0.5297e-10 |
0.5311e-10 |
0.5304e-10 |
|
- |
2.1210e-10 |
1.1906e-10 |
0.9439e-10 |
0.8282e-10 |
0.7648e-10 |
|
- |
- |
4.7762e-10 |
2.1187e-10 |
1.4749e-10 |
1.1931e-10 |
|
- |
- |
- |
8.4887e-10 |
3.3118e-10 |
2.1245e-10 |
|
- |
- |
- |
- |
13.2746e-10 |
4.7723e-10 |
|
- |
- |
- |
- |
- |
19.1207e-10 |
The grayed values coincide with the Bohr/Schrodinger orbits.
The energy of those orbits is found using the sum of the kinetic and potential energy, EK and EP.
E = EK + EP = 0.5mse2 + [-e2/(4pe0r)] from equation 6: se = (e2/4pme0r)0.5
E = 0.5me2/4pme0r - e2/4pe0r
E = e2/8pe0r - e2/4pe0r
E = -e2/8pe0r [J]orE = -e/8pe0r [eV]
For n = 1 through 6 the energy of each radii in eV are:
|
n = 1 |
n = 2 |
n = 3 |
n = 4 |
n = 5 |
n = 6 |
|
-13.6081 |
-13.6390 |
-13.5645 |
-13.5927 |
-13.5568 |
-13.5747 |
|
- |
-3.3946 |
-6.0474 |
-7.6280 |
-8.6936 |
-9.4143 |
|
- |
- |
-1.5075 |
-3.3983 |
-4.8817 |
-6.0347 |
|
- |
- |
- |
-0.8482 |
-2.1741 |
-3.3890 |
|
- |
- |
- |
- |
-0.5424 |
-1.5087 |
|
- |
- |
- |
- |
- |
-0.3766 |
1.5 Forces at the Orbits
We now want to consider the forces encountered by an electron as it spirals toward the proton nucleus. We begin by relating the electrostatic (Fe), centripetal (Fc) and extra-nuclear forces (i.e. forces exerted from space, Fs). We'll adopt a convention that positive forces move the electron toward the nucleus and those that move the electron away are negative.
Fs + Fe - (Fc) = 0
Fs + e2/4pe0r2 - mse2/r = 0
mse2/r = Fs + e2/4pe0r2
se/c = (Fsr/m + e2/4pme0r)0.5/c
Recalling Equation 5 and the substitution that h = se/c:
sin((h/a)( np + -1nq)) = (Fsr/m + e2/4pme0r)0.5/c
c2sin2((h/a)( np + -1nq)) = Fsr/m + e2/4pme0r
Fs = [(mc2/r)sin2((h/a)( np + -1nq))] - e2/(4pe0r2) Equation 9
Since h and r are related it would be convenient to have an equation where h is a function of r. We start by recognizing that h = se/c = sinqe. Using equation 8, we'll focus on finding qe:
r = K / (tanqesinqe)
b = K / r = tanqesinqe
b = sin2qe/cosqe where: tan() = sin()/cos()
b = (1 - cos2qe)/cosqe where: sin2() = 1 - cos2()
b cosqe = 1 - cos2qe
cos2qe + b cosqe - 1 = 0
cosqe = (-b + (b2 + 4)0.5) / 2 NOTE: real root from quadratic formula retained
qe = acos[(-b + (b2 + 4)0.5) / 2]
From here it is a simple matter to find h:
h = sinqe
h = sin(acos[(-b + (b2 + 4)0.5) / 2])
h = sin(acos[(-(K/r) + ((K/r)2 + 4)0.5) / 2]) Equation 10
Equations 9 and 10 are then used to plot the force on the electron. What is immediately apparent is the stable operating point at each orbital radius. As the electron spirals in under the influence of the positive force, it begins to encounter a negative force (i.e. a force that pushes the electron outward - see Figure 4a). What is also interesting, is that with each successive stable orbit, the negative force is diminished, leading to the consequence that orbits further from the nucleus are less stable (see Figure 4b).
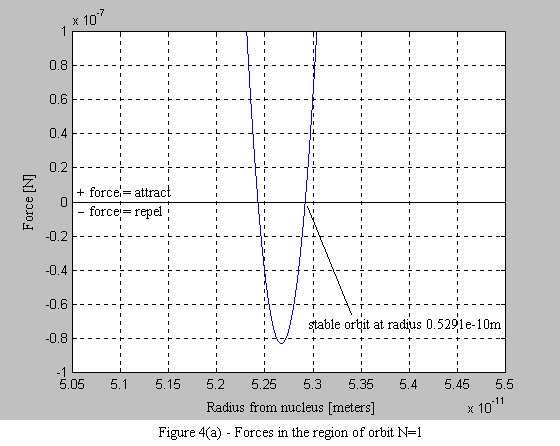
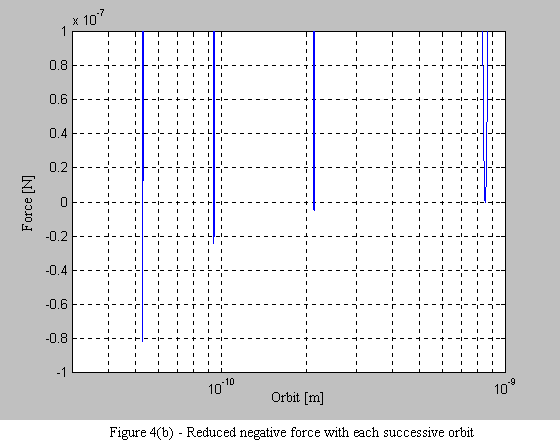
1.6 Conclusion
What has been viewed as a condition of nature we "just had to accept", has been shown to be derivable from Rutherford's "planetary" model. The mechanisms responsible for the discrete orbits of the electron lies in the time delay associated with momentum transferred by the electric field between the particles combined with the effect relativity has on the electron's mass affecting its momentum. This time delay is comprised of three components - the distance between the particles, the mass of the proton (section 1.2) and the time dilation caused by the electric field.
Appendix 1: MATLAB File for Figure 1